LeetCode - 二叉树的层序遍历 / 轮转数组

二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

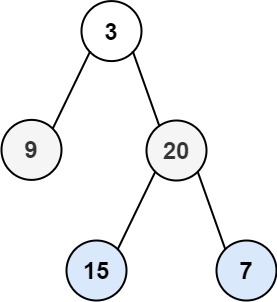
示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

解题思路

核心思路

使用队列按层遍历二叉树，确保同一层的节点被连续处理，并正确收集每一层的节点值。

算法步骤

1. 初始化

ArrayList<List<Integer>> all = new ArrayList<>();
if(root == null){
    return all;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);

• 创建结果列表 all 存储所有层的遍历结果

• 创建队列 queue 存储待处理的节点

• 将根节点加入队列，作为遍历的起点

2. 主循环（逐层处理）

while(!queue.isEmpty()){
    int size = queue.size();  // 关键：记录当前层的节点数
    ArrayList<Integer> sub = new ArrayList<>();
    
    for(int i=0; i<size; i++){  // 处理当前层的所有节点
        TreeNode node = queue.poll();
        sub.add(node.val);
        
        // 将下一层的节点加入队列
        if (node.left != null) {
            queue.add(node.left);
        }
        if (node.right != null) {
            queue.add(node.right);
        }
    }
    all.add(sub);  // 保存当前层的结果
}

完整代码

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList<List<Integer>> all = new ArrayList<>();
        if(root == null){
            return all;
        }
		LinkedList<TreeNode> queue = new LinkedList<>();
		queue.add(root);

        while(!queue.isEmpty()){
            int size = queue.size();
            ArrayList<Integer> sub = new ArrayList<>();
            for(int i=0;i<size;i++){
                
                TreeNode node = queue.poll();
                sub.add(node.val);
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
            all.add(sub);
        }
		return all;
	}
}

轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：

• 1 <= nums.length <= 105

• -231 <= nums[i] <= 231 - 1

• 0 <= k <= 105

解题思路

额外数组空间两段复制

使用额外数组存储旋转后的结果，然后复制回原数组。

算法步骤详解

1. 创建新数组

int[] newNums = new int[nums.length];

• 创建一个与原数组相同大小的新数组

• 用于存储旋转后的结果

2. 计算新位置并填充

for (int i = 0; i < size; i++) {
    int newIndex = (i + k) % size;
    newNums[newIndex] = nums[i];
}

关键逻辑：

• 对于原数组的每个元素 nums[i]

• 计算它在旋转后的新位置：(i + k) % size

• 将元素放到新数组的对应位置

3. 复制回原数组

System.arraycopy(newNums, 0, nums, 0, size);

• 将新数组的内容复制回原数组

• 使用 System.arraycopy 提高效率（原生方法）

完整代码

public class Solution {
    public void rotate(int[] nums, int k) {
        int[] newNums = new int[nums.length];
        int size = nums.length;

        for (int i = 0; i < size; i++) {
            int newIndex = (i + k) % size;
            newNums[newIndex] = nums[i];
        }
        System.arraycopy(newNums, 0, nums, 0, size);
    }
}