环形链表

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

示例 1：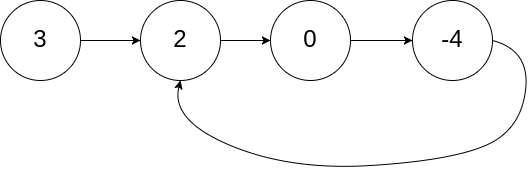

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：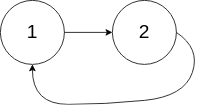

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

• 链表中节点的数目范围是 [0, 104]

• -105 <= Node.val <= 105

• pos 为 -1 或者链表中的一个 有效索引 。

解题思路

通过 快慢指针 的追逐来判断链表是否有环：

1. 慢指针（next）：每次移动 1 步。

2. 快指针（nextNext）：每次移动 2 步。

如果链表有环，快指针最终会追上慢指针（即两者相遇）；如果无环，快指针会先到达链表末尾（null）。

代码分步解析

1. 初始检查

if (head == null || head.next == null) {
    return false;
}

• 作用：处理边界情况。

  • 空链表（head == null）或单节点链表（head.next == null）直接返回 false（无环）。

2. 初始化指针

ListNode nextNext = head.next;  // 快指针（初始位置：head.next）
ListNode next = head;          // 慢指针（初始位置：head）

• 初始位置：快指针比慢指针 超前一步（避免首次循环时误判）。

3. 循环判断

while (next != nextNext) {  // 当快慢指针未相遇时继续移动
    if (nextNext == null || nextNext.next == null) {
        return false;       // 快指针到达末尾，无环
    }
    nextNext = nextNext.next.next;  // 快指针移动2步
    next = next.next;               // 慢指针移动1步
}
return true;  // 快慢指针相遇，有环

• 终止条件：

  • 有环：快慢指针相遇（next == nextNext），返回 true。

  • 无环：快指针遇到 null（链表末尾），返回 false。

完整代码:

public class Solution {
	public boolean hasCycle(ListNode head) {
		if (head == null || head.next == null) {
			return false;
		}

		ListNode nextNext = head.next;
		ListNode next = head;

		while (next != nextNext) {
			if (nextNext == null || nextNext.next == null) {
				return false;
			}
			nextNext = nextNext.next.next;
			next = next.next;
		}
		return true;
	}
}

翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内

• -100 <= Node.val <= 100

解题思路

翻转二叉树（也叫镜像二叉树）是指将二叉树的每个节点的左右子树都进行交换。代码采用后序遍历的递归方式：

1. 基线条件：如果当前节点为null，直接返回（递归终止条件）

2. 递归翻转左子树：invertTree(root.left)

3. 递归翻转右子树：invertTree(root.right)

4. 交换左右子树：将当前节点的左右指针互换

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return root;
        }

        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);

        root.left = right;
        root.right = left;
        return root;
    }
}